密码学可以追溯到两千多年前的凯撒大帝,他发明了一种加密方式把明文的每个字符向后移动3位。为了方便理解,假设凯撒大帝说英语,用字母a-z写信,那么如果凯撒大帝想写一封内容为helloworld的信,他加密后的内容应该是khoorzruog。
为了方便运算,把a-z映射为数字0-25那么凯撒密码可以表示为f(p)=(p+3)mod 26。符号mod表示模运算,意思是除26取余数。比如信中的h对应数字7,f(8)=(7+3)mod 26=10对应字符k。有加密就有解密,解密就是把加密的过程反过来p=(f(p)-3)mod 26。
可以用更加通用的公式表示凯撒密码f(p)=(p+k)mod 26其中k叫做安全密钥,持有相同密钥的双方可以正常加解密通信。
随着密码学的出现,同时出现了另两项技术密码分析和密码破译,光与暗总是相生相伴。其中一种破译方式是对比字符出现的概率,通过一些语料可以统计出字符的出现概率这个是已知的。然后统计出密文出现频率最高的字符,然后假设这两个字符相等,解出k然后进行解密,看看解出来的文字是否有意义,如果有意义认为破解完成,如果没有意义换一个字符继续试。
凯撒密码很容易被破解,直接爆破都行,反正就26个字母。那么就需要对凯撒密码进行加固,一种方式是调整加密公式为f(p)=(ap+b)mod 26,叫做仿射密码(affine ciphers),加密过程依然简单,但是解密过程没有那么直观。
为了解密这里引入同余式的概念,假设a mod m=b mod m那么就记为
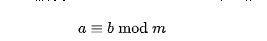
同余式满足一些定理。
假设有2个同余式

那么
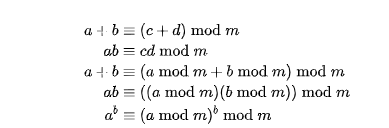
这个和四则运算有点像,同样的也满足交换律、结合律和分配律。四则运算还有两个逆元:加法逆元和乘法逆元(倒数),模运算里面也有,而且这个乘法逆元是上述解密时要用的。
a模m的乘法逆元和a满足等式

假设密文是d为了解出p相当于解方程

根据前面提到的定理我们可以知道

解密的重任落到了如何求解a模m的乘法逆元上。这时候需要最大公约数上场,在我的印象中求解最大公约数的方法叫辗转相除法,就是两个数交替取余数。比如10,24的最大公约数是

所以最大公约数gcd(10,24)=2。这种算法还有一个名字叫欧几里得算法,2000多年前就有记载了。
和最大公约数有关的还有个贝祖定理:如果a b是正整数,那么存在s t使得gcd(a,b)=sa+tb成立,(s,t)叫做贝祖系数。
回到乘法逆元,我们先假设gcd(a,m)=1那么根据贝祖定理存在(s,t)使得等式sa+tm=1成立,tm肯定整除m那么

也就是说贝祖系数中的s就是我们需要的a模m的乘法逆元,问题转到如何求贝祖系数了。
贝祖系数的一种解法是把辗转相除法倒过来再算一遍(还有很多别的算法)。以gcd(10,24)为例,辗转相除法的3个等式也可以写成

最后一个等式丢弃不用,从倒数第二个开始,把上一个等式带入到下一个等式中,得到
2=10-4*2=10-(24-10*2)*2=5*10-2*24
那么贝祖系数就是(5,-2)也就是说gcd(10,24)=5*10+(-2)*24
到此解密需要的要素都集齐了。实际来用一下假设加密算法是f(p)=(7p+3)mod 26,gcd(7,26)=1乘法逆元一定存在,假设收到的密文是8需要解密出原文是多少。

首先算出贝祖系数,先来一遍辗转相除法

丢弃最后一个等式不用,开始按顺序倒着代入得到

得出(7,26)的贝祖系数是(-11,3)也就是7模26的乘法逆元是-11。现在收到的密文是8代入解密公式

因为0<=p<26所以p=23。
当然针对这个例子还有一个更简单的解法,p的取值范围就[0,26)一共不过26个值,按照加密公式算出所有密文,保存到表里,要用的时候select一下就好了,哈希加密的破解用了类似方式,叫彩虹表(rainbow table)来着。
前面的加密算法都是对单个字符进行加密,为了更强的安全性,开发出分组密码(block ciphers)这种方式不再以单个字符为单位进行加密,而是以一组字符为单位进行加密。比如4个字符组成一组那么helloworld就可以分成3组,分别是he llow orld然后每个字符用2个数字表示,比如a=00,b=01,...,z=25分组的字符可以表示为0704 11111422 14171103在然后对这3组数字进行加密,这时候再统计密文频率,只能统计个寂寞。
凯撒密码和仿射密码都是私钥密码系统。这种密码系统只要知道了私钥,那么加密解密的过程都知道了。与之相对的还有公钥密码系统,比如RSA密码。
RSA密码在我接触的项目中用的比较多,数据比较敏感的接口可能就会用上,比如支付啥的。RSA秘钥有2个,公钥和私钥。公钥公开,交给对方用来加密数据,私钥自己保存用来解密。
RSA的工作原理是这样的,生成5个数p q n e d其中p q是两个很大的质数。这5个数满足两个等式
假设m是明文,c是密文

RSA加密算法

RSA解密算法

为了证明RSA加解密算法是正确的需要用到费马小定理。
费马小定理的描述是对于质数p任何不整除p的整数m满足等式

然后开始操作

因为p q互质

m的取值范围是[0,n)所以

也就是解密算法。对于RSA密码系统来说n e c这3个信息是暴露的,但是解密需要的d要通过p q来计算,对于破解者来说先通过n分解出p q这是非常庞大的计算量,运行时间至少是按年来算的,所以在超级牛逼的计算机出来前RSA算法是安全的,另外定期更换密钥是好习惯。第一次看到这里的时候震惊了,万万没想到本来一个无解的东西居然也能被利用起来。
为了求证下,我用python库cryptography读取了本地ssh-keygen生成的公钥和私钥,的确是这么回事。

输出的结果里除了e其他几个数字都巨长。

这几个数字都很大,直接用二进制表示肯定会溢出,刚好余数可以用来表示很大的数,这块会用到中国余数定理。
中国余数定理在《孙子算经》里有描述
今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
答曰:二十三。
术曰:三三数之剩二,置一百四十;五五数之剩三,置六十三;七七数之剩二,置三十,并之,得二百三十三。以二百一十减之,即得。凡三三数之剩一,则置七十;五五数之剩一,则置二十一;七七数之剩一,则置十五。一百六以上,以一百五减之,即得。
问题翻译过来就是求解x满足同余式

答案翻译过来就是140+63+30-210=23。它求得是最少的数量。后半句是解题思路:就是说余数是x,y,z时,计算70x+21y+15z结果超过106就-105直到小于106。
反过来理解23可以用(2,3,2)来表示,而且运算也可以通过余数来计算,比如7可以表示为(1,2,0)那么23+7=(2+1,3+2,2+0)=(0,0,2)。根据这个思路可以挑几个比较大的两两互质的数,比如
这3个数就可以表示2的100次方以内的数了,而且还可以运算,数学真是门神奇的学科。
上面的内容参考《离散数学》第4章,书上有更多更详细的内容,感兴趣的小伙伴可以一看,还是有很多有趣的东西的。
题图:Photo by Bella White from Pexels

