此文为深兰科学院密码芯片研发组撰写。文章将为大家从量子密码学的背景、量子密码学的原理、BB84量子秘钥分发协议介绍和实现思路,以及量子密码技术的应用场景等方面讲述量子密码技术的基本概况。
量子密码学背景
Quantum Cryptography
近些年,随着社会网络的普及,大数据、云计算等各类新技术的迅猛发展,信息安全问题愈发引人关注。对于政府和企业而言,商业往来、政府行政、外交军事等都依赖密码技术,如何将信息转化为只有特定的人才能解读的编码是至关重要的问题。与此同时,传统密码技术也存在着固有缺陷,当未来计算机计算能力的不断增强和新算法的提出,这将会大幅增加信息泄露的风险。在此大环境下,探索思考更优的密码技术方案是数字时代的发展趋势,量子密码学也相应而生。它利用了量子的强大特性,为实现无条件安全性提供了全新的可行性。
量子密码学原理
测不准原理(量子世界粒子运动规律)
微观世界的粒子有许多共轭量(位置和速度)。在某一时刻,人们只能对一个共轭量之一进行测量,不能同时测量另一个与之共轭的量。更加奇怪的是,量子态叫做「只能测一次」。只要对任何一个量子态做一次测量,那个量子态就会坍塌,彻底变成另外一个状态;那么不会有第二次机会。
不可克隆定理
量子的世界不同于经典的世界,经典的世界复印机可以复印相同的一份文件;但是在量子世界却不存在,复制后将破坏原来的量子态。
量子纠缠特性
两个纠缠的量子,无论相隔多远,改变其中一个量子状态时,另一个量子会在瞬间发生状态变化。
光子偏振
1:定义
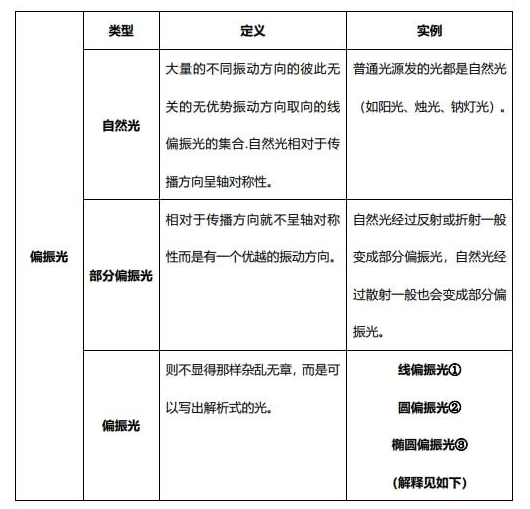
偏振光:当两个频率相同,振动方向相垂直的单色波相叠加时,产生的就是偏振光。
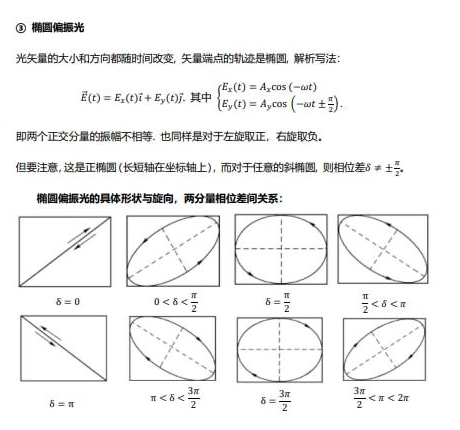
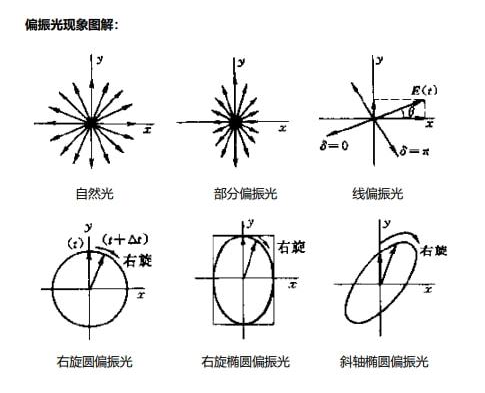
2:偏振光现象


BB84量子密钥分发协议
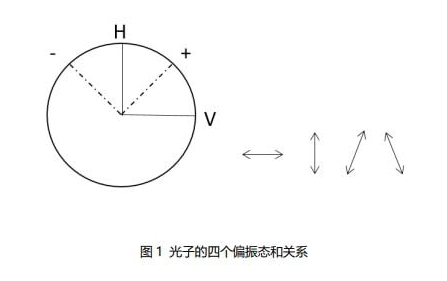
1984年,Bennett(贝内特)和Brassard(布拉萨德)最早提出了量子密码协议-BB84协议。该密码术与经典密码最大区别是它能抵挡任何破译技术和计算工具的攻击,原因在于它的安全性是由物理定律来保证,而不是靠某种高复杂的运算。BB84协议通过光子的4种偏振态来进行编码:线偏振态,圆偏振态,如图1所示。其中,线偏振光子和圆偏振光子的两个状态各自正交,但是线偏振光子和圆偏振光子之间的状态互不正交。
BB84协议实现通道
BB84协议的实现需要两个信道,经典信道和量子信道
经典信道:确保收发双方Alice和Bob之间能进行一些必要信息的交换
量子信道:传输携带信息的或者随机的量子态
BB84协议的实现思路
BB84量子秘钥分发协议(理想情况)
(1)发送方Alice随机产生一组二进制序列sA。假定该序列为8 bit,数值为[01100101]。Alice再生成另一组相同长度的随机序列mA。
(2)假定mA数值为[10111100]。这就是在量子信道中(比如在光纤中)发送的序列。根据这两个序列,调制产生8个光子。根据以下表1中的关系确定如何调制每个光子的状态,具体状态如图2中所示。
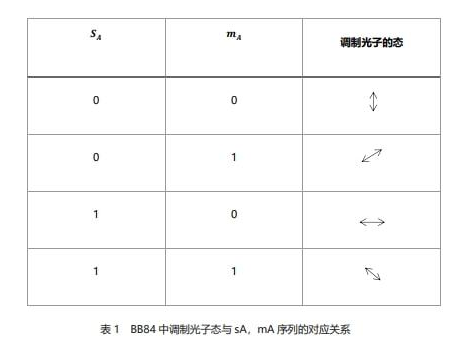
(3)接收方Bob并不知道应该用哪组基进行测量,所以Bob生成一个随机序列用来选择测量基。假定测量基序列mB,数值为[00101010]。按照以下表2的关系选择测量基,对粒子测量。
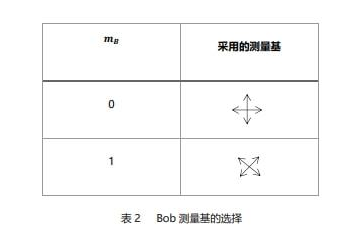
然后Bob通过经典信道通知Alice他所选定的测量基序列mB。Alice比较Bob的测量基序列mB和她自己保留的发送基序列mA,并且通知Bob所采用的测量基中相同与不同的值。Alice和Bob分别保存其中测量基一致的测量结果,并且放弃其中测量基不一致的测量结果。根据所选用的测量基序列的出错率判定是否存在攻击,如果异常则中止协议。
(4)Alice和Bob按照下面的方式将量子态编码成二进制比特:和表示0,和表示1,获得原始密钥。
(5)Alice和Bob获得相同的密钥序列kA和kB。
BB84协议实现思路的简要步骤图(理想情况):
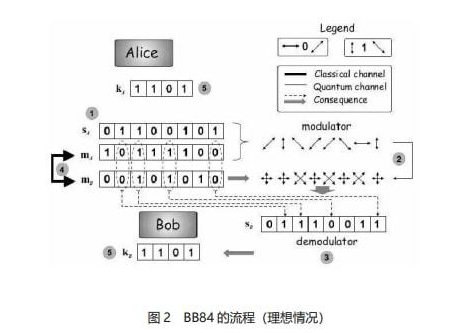
BB84量子密钥分发协议(存在窃听情况):
图3中给出了存在Eve窃听的情况,也就是说Eve拦截了传输的光子,进行测量,然后再自己调制出光子发送到Bob。
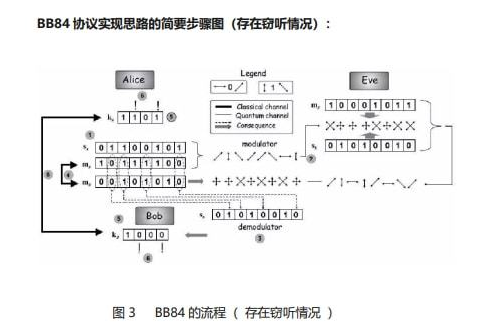
(1)Eve也不知道应该用哪组基进行测量,故用自己的序列mE作为测量基选择,这样得到结果sE,比如[01010010]。
(2)Eve根据sE和mE重构光子并传输给Bob。
注意到,这里就必将会引入错误,因为sA、mA和sE、mE从概率上不可能完全相同。这样,通过图3中第六步Alice和Bob之间的比较验证,即通过选取一些Key进行比较,就可以发现Eve的存在。而在实际操作中会更加复杂,采用纠错处理、保密增强等方法对原始密钥作进一步处理,以提高密钥的保密性,并最终获得安全密钥。
无条件安全性
测不准原理和量子不可克隆定理保证了BB84协议量子通信的无条件安全性。
测不准原理
在BB84协议中,所采用的线偏振和圆偏振是共扼态,满足测不准原理。根据测不准原理,线偏振光子的测量结果越精确意味着对圆偏振光子的测量结果越不精确。因此,任何攻击者的测量必定会对原来量子状态产生改变,而合法通信双方可以根据测不准原理检测出该扰动,从而检测出与否存在窃听。
不可克隆定理
另外,线偏振态和圆偏振态是非正交的,因此它们是不可区分的,攻击者不可能精确地测量所截获的每一个量子态,也就不可能制造出相同的光子来冒充。
量子密码技术应用场景
世界首次传输基因组数据
日本电子巨头东芝公司和东北大学宣称,实现了世界上首次使用量子密码技术来传输基因组序列数据的方法,已经成功使用量子密码技术传输了24个人的完整基因组序列数据,这在理论上是一种坚不可摧的加密方法。这是使量子密码向商业化迈进的关键一步。根据日本的法律,有关个人的基因组数据在某些情况下被视为受保护的个人信息,并使用指纹扫描仪在生物识别硬盘中进行物理传输。而量子加密技术可以使其通过光缆进行传输。该测试使用东芝公司开发的设备,使用光子发送加密的数据和解码所需的密钥。
非法读取数据的任何尝试都会改变光子的量子状态。目前的量子计算技术通常要求温度接近绝对零度,而东芝的加密设备可以在室温下运行。由于光子能量会随着传输距离的增长而损失,因此,在量子密码术中保持快速的传输速度成了一大挑战。为了克服这个问题,数据在传输过程中被分成小段进行加密,而不是一次性全部加密。在整个测试过程中,从发送整个基因组数据到解密这一过程没有超过两分钟。
高级密码学——量子同态加密(QHE)
2013年,Liang首次提出量子同态加密(Quantum homomorphic encryption,QHE)的思想,并构造了一个对称量子全同态加密(Quantum fully homomorphic encryption,QFHE)方案。与经典同态加密相比,量子同态加密的安全性更高。
2015年美密会上,Broadbent和Jeffery正式给出了QHE在公钥加密和对称加密系统下的定义,并将标准模型下的语义安全扩展到量子模型下的语义安全。
2016年美密会上,Dulek等人提出了紧凑型QHE方案DSS16,方案能够高效同态运行任意多项式级别的量子电路。
2018年,Goyal等人在DSS16方案基础上,提出了量子多密钥同态加密的概念,并且构造了从经典的层次型多密钥同态加密到量子层次型多密钥同态加密的通用转化方法。
金融业应用分析
基于量子密钥技术重新构建新的应用平台,利用量子密钥技术进行通信加解密处理的核心过程如下:
(1)信息发送者和信息接收者事先向量子密钥分发机构申请注册。
(2)信息发送者在发送信息前,实时向量子密钥分发机构请求获得一次性量子密钥。
(3)量子密钥分发机构实时调用通信卫星提供的服务,在信息发送者和接收者之间实次性随机密钥的交换处理。
(4)发送者使用该密钥,利用传统的对称加密算法,对信息正文进行加密。
(5)密文通过传统信道传送给接收者。
(6)接收者使用相同密钥进行解密。
上述信息发送者和信息接收者,都可以是银行同业;或者是银行与客户。
参考文献
1.BB84原文发在量子研究网站上:http://quantum-study.com/article/978/22.html)
2.C.H.Bennett,G.Brassard,Quantum cryptography:Public key distribution and coin tossing,in Proc.Int.Conf.Comput.Syst.Signal Process,1984,175~179
3.Sandor Imre,Ferenc Balazs,Quantum Computing and Communications-An Engineering Aproach,John Wiley&Sons,Ltd,2005
4.李宁波,周潭平,车小亮,杨晓元,韩益亮.多密钥全同态加密研究[J].密码学报,2020,7(6):713–734.[DOI:10.13868/j.cnki.jcr.000401]
5.Quantum Multi-Key Homomorphic Encryption for Polynomial-Sized Circuits(Rishab Goyal)
6.LIANG M.Symmetric quantum fully homomorphic encryption with perfect security[J].Quantum Information Processing,2013,12:3675–3687.[DOI:10.1007/s11128-013-0626-5]
7.BROADBENT A,JEFFERY S.Quantum homomorphic encryption for circuits of low T-gate complexity[C].In:Advances in Cryptology—CRYPTO 2015,Part II.Springer Berlin Heidelberg,2015:609–629.[DOI:10.1007/9783-662-48000-7_30]
8.DULEK Y,SCHAFFNER C,SPEELMAN F.Quantum homomorphic encryption for polynomial-sized circuits[C].In:Advances in Cryptology—CRYPTO 2016,Part III.Springer Berlin Heidelberg,2016:3–32.[DOI:10.1007/9783-662-53015-3_1]
9.GOYAL R.Quantum multi-key homomorphic encryption for polynomial-sized circuits[J].IACR Cryptology ePrint Achieve,2018:2018/443.https://eprint.iacr.org/2018/443.pdf

